이 논문은 Knowledge Distillation의 초기 논문으로 많이 소개되는 논문입니다.
논문이 나올 당시에는 computing power가 좋지 않았고, 당시에도 모델은 점점 거대해지고 generalization을 위해 ensemble 모델을 사용하는 방향으로 연구되어 왔습니다.(지금은 더 거대한 모델도 더 적은 시간으로 학습 시킬 수 있지만) 그 과정에서 저자는 높은 accuracy를 위해 엄청난 시간이 걸려서 학습시키는 것이 비효율적이라고 생각하게 됩니다. 그래서 거대한 ensemble 모델의 ‘knowledge’를 작은 모델로 ‘distillation’해서 모델의 크기를 줄이고자 합니다.
Distillation(증류)이란 액체 혼합물을 분리하는 방법 중 하나입니다. 끓는점을 이용하므로 일반적으로 가열해 혼합물을 분리하게 됩니다. 이와 비슷하게 불필요하게 많은 parameter를 가진 모델에서 실제로 필요한 knowledge만을 분리해 모델의 크기를 줄이는 것을 의미합니다.
distillation은 argmax와 같은 함수를 통해 하나의 답을 output으로 내기 전과 같이 abstraction 단계를 하나 올라가서 그 값을 활용합니다. 모델을 하나의 함수로 생각하고 input 벡터와 output 벡터의 mapping이라고 생각하는 것입니다. 도츨된 답이 아니라 벡터로 표현된 확률분포를 학습하는 것입니다. 정답이 아닌 것의 상대적인 확률도 어떠한 정보를 가지고 있다고 보는 것이죠. 헷갈리기 쉬운 클래스들 일 수록 상대적으로 다른 클래스들에 비해 높은 확률을 가질 것이기 때문입니다.
모델은 보통 학습 데이터의 최적값을 구하게 됩니다. 실제로는 새로운 데이터에 잘 일반화되는 것이 목적인데 말이죠. 이 논문에서는 distillation을 통해서 거대한 모델의 일반화 방법을 학습시킬 수 있다고 말합니다.
이것의 구체적인 방법이 ‘soft target’ 입니다.
Soft Target
distillation은 softmax layer를 수정하여 아래와 같은 soft target을 얻습니다.
\[q_{i}=\frac{exp(z_{i}/T)}{\sum_{j} exp(z_{j}/T)}\]이러한 temperature($T$, soft target)를 사용하게 되면 확률분포를 보다 부드럽게 해주는 효과 있습니다.일종의 smoothing 효과라고 볼 수 있습니다. $T$가 무한대에 가까워질 수록 $q$는 $\frac{1} {n}$에 가까워진다는 것입니다. 아래의 예시를 보면 쉽게 알 수 있습니다.(그림 그려서 넣기)
\[softmax\begin{pmatrix} 1 \\ 3\\ 9 \end{pmatrix} = \begin{pmatrix} 0.0003345 \\ 0.0024718\\ 0.9971937 \end{pmatrix}, softmax_{T=3}\begin{pmatrix} 1 \\ 3\\ 9 \end{pmatrix} = \begin{pmatrix} 0.057 \\ 0.112\\ 0.830 \end{pmatrix}\]학습 방법
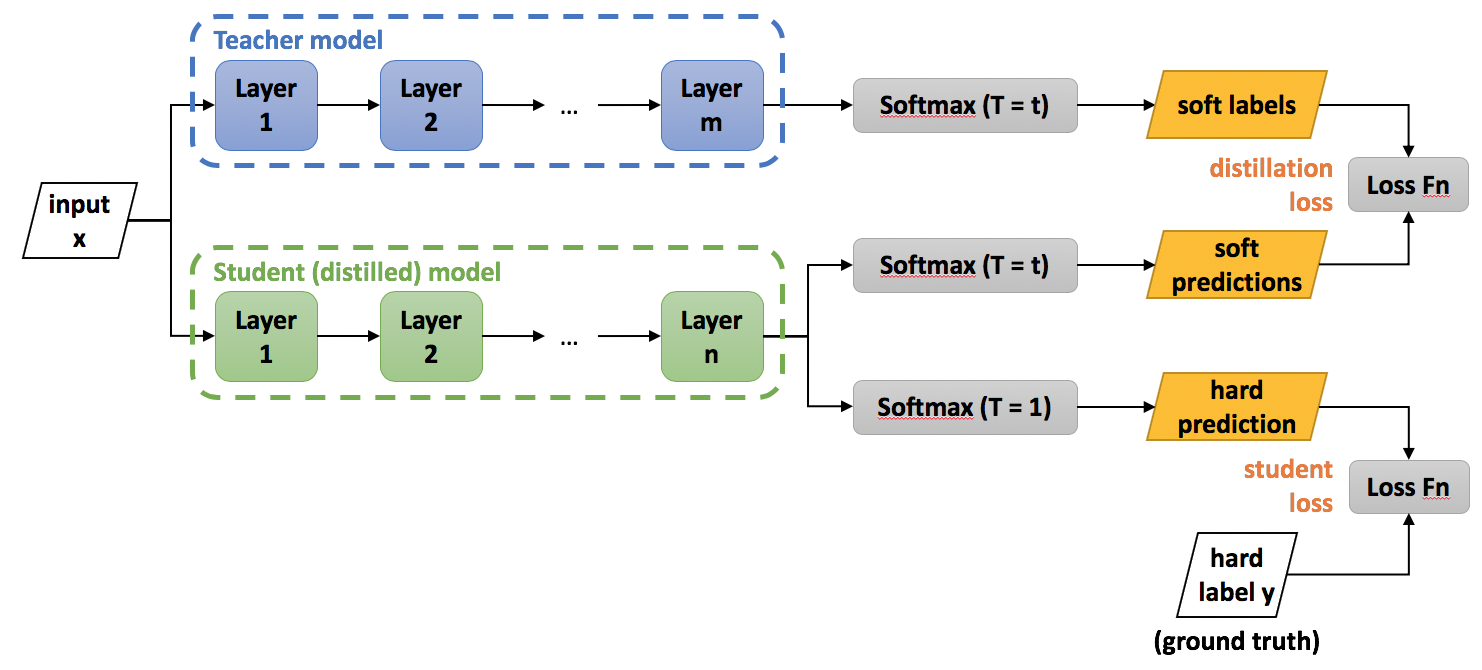
논문에서 loss function에 대해서는 구체적인 수식을 제시하고 있지는 않지만, Similarity preserving knowledge distillation 논문과 코드 등을 참고하여 생각해보면 다음과 같습니다. (개인적으로 해당 깃허브에 다양한 KD가 구현되어 있어서 공부하기에 좋다고 생각합니다.)
\[Total Loss = (1-\alpha)L_{CE}(\sigma (Z_{s}), \widehat{y}) + \alpha T^{2}L_{CE}(\sigma (\frac {Z_{t}}{T}), \sigma (\frac {Z_{s}}{T})) \\ \\ L_{CE}(): Cross \ entropy \ loss \\ \sigma (): \ Softmax \\ Z_{s}: \ Output \ logits \ of \ Student \ network \\ Z_{t}: \ Output \ logits \ of \ Teacher \ network \\ \widehat{y}: \ Ground \ Truth \\ \alpha: \ Balancing \ parameter \\ T: \ Temperature \ hyperparamter\]높은 temperature를 이용해 얻은 큰 모델과의 cross entropy 와 정답 label을 사용해 얻은 crossentropy 둘을 가중치를 주어 이용할 수 있습니다. 후자에 낮은 가중치 주어야 더 나은 결과가 나왔다고 합니다. 또한 이런 방법을 사용할 때에는 soft target에 의해 계산된 기울기는 $1/T^{2}$의 스케일을 가지므로 soft target에 $T^{2}$을 곱해줍니다.
왜 soft target의 기울기가 $1/T^{2}$인지 조금 더 생각해보겠습니다. soft target의 cross entropy를 역전파를 위해 미분하면 아래와 같습니다. ($z_{i}$ : logit of distilled model, $v_{i}$ : logit of cubersome model)
\[\frac{\partial C}{\partial z_{i}}=\frac{1}{T}(q_{i}-p_{i})=\frac{1}{T}(\frac{e^{z_{i}/T}}{\sum_{j}e^{z_{i}/T}}-\frac{e^{v_{i}/T}}{\sum_{j}e^{v_{i}/T}})\]$e^{x}$을 taylor series로 근사시키면 $e^{x}=1+x+\frac {x^2}{2!} + \cdots$ 이므로 아래와 같은 식이 됩니다.
\[\frac{\partial C}{\partial z_{i}} \approx \frac{1}{T}(\frac{1+z_{i}/T}{N+\sum_{j}z_{j}/T}-\frac{1+v_{i}/T}{N+\sum_{j}v_{j}/T})\]
Reference
- Distilling the Knowledge in a Neural Network, Hinton, J.Dean, 2015
- https://intellabs.github.io/distiller/knowledge_distillation.html
- Similarity-Preserving Knowledge Distillation, Frederick Tung, Greg Mori, 2019