문제 : boj 2225
풀이
- 배열 _sum[k][n]는 k번 더했을 때, n의 값이 나오는 경우의 수를 의미한다.
- _sum[k][n]은 k-1번 더했을 때 n 이하의 값을 가지는 모든 경우의 수이다. 아래 그림과 같이 n이하의 값을 가지는 경우의 수 각각에 0 ~ n 중에 필요한 만큼을 더해주면 n의 값을 얻는다.
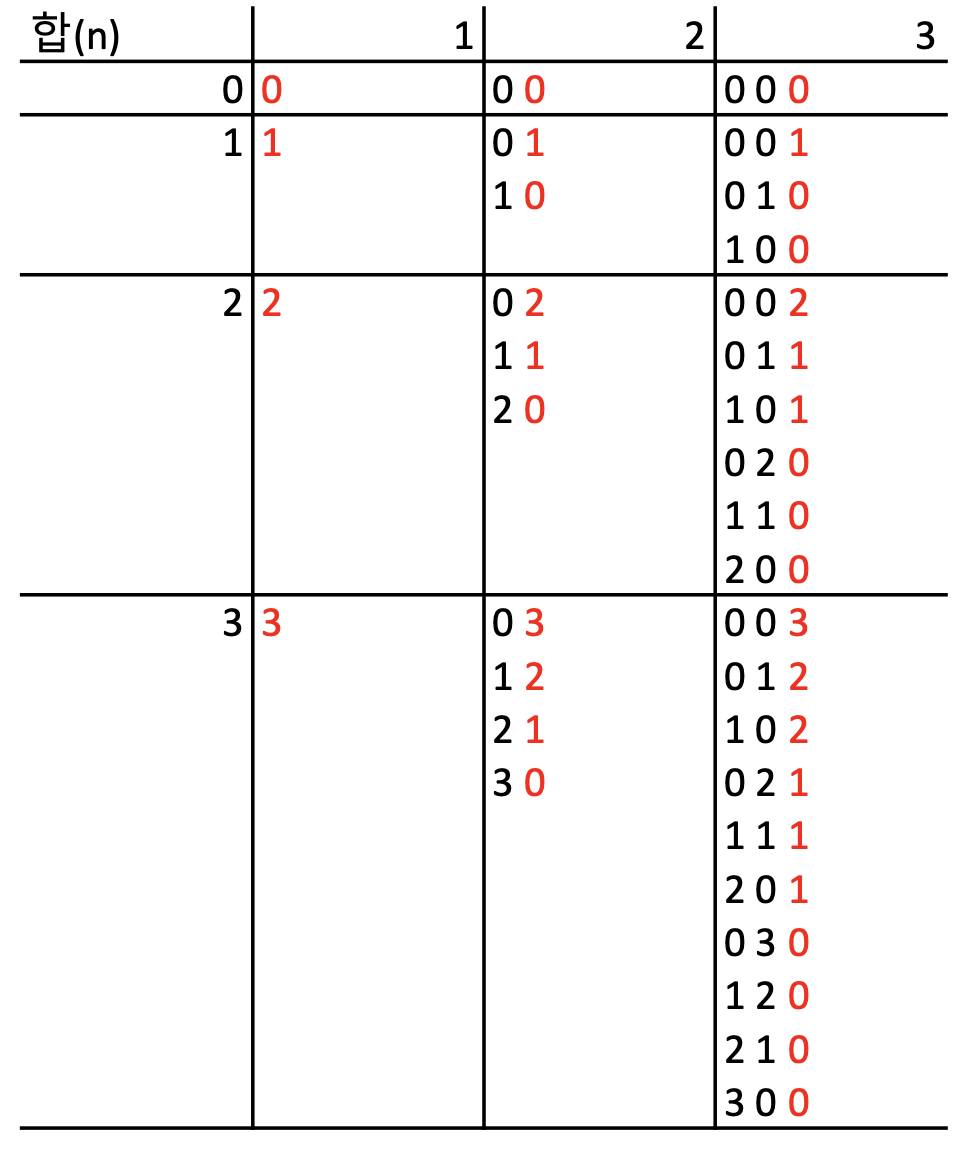
- k-1번 더했을 때, n 이하의 값을 가지는 모든 경우는 _sum[k]의 배열 값을 n 번째 까지 더한 것이고, _sum[k][n-1]이 이미 n-1 번째 까지의 합을 가지고 있으므로 _sum[k][n] = _sum[k][n-1] + _sum[k-1][n] 의 점화식을 가지게 된다.
C++
#include <iostream>
using namespace std;
int dp(const int N, const int K){
int _sum[K+1][N+2];
for (int k(1); k < K+1; k++){
for (int n(0); n < N+1; n++){
_sum[k][n] = 0;
}
}
for (int k(1); k < K+1; k++){
for (int n(0); n < N+1; n++){
if(k == 1 | n == 0) _sum[k][n] = 1;
else {
_sum[k][n] = (_sum[k-1][n]+_sum[k][n-1])%1000000000;
}
}
}
return _sum[K][N];
}
int main(){
int N, K;
cin >> N >> K;
cout << dp(N, K);
}
+) 배열을 _sum[N]으로 만들어서 _sum[n] = _sum[n] + _sum[n-1]으로 사용하면 더 적은 메모리를 사용할 수 있다.